一、LRU 缓存机制概念
缓存淘汰算法
LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently Used,也就是说我们认为最近使用过的数据应该是「有用的」,很久都没用过的数据应该是无用的,内存满了就优先删那些很久没用过的数据。核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高
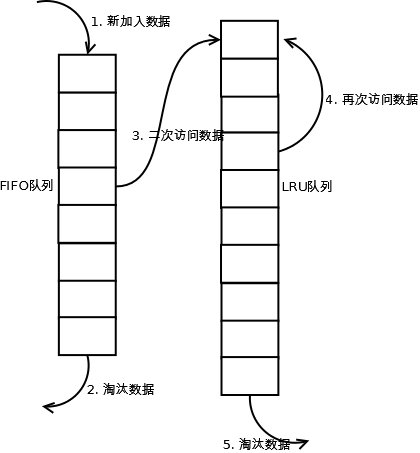
- 新数据插入到链表头部;
- 每当缓存命中(即缓存数据被访问),则将数据移到链表头部;
- 当链表满的时候,将链表尾部的数据丢弃。
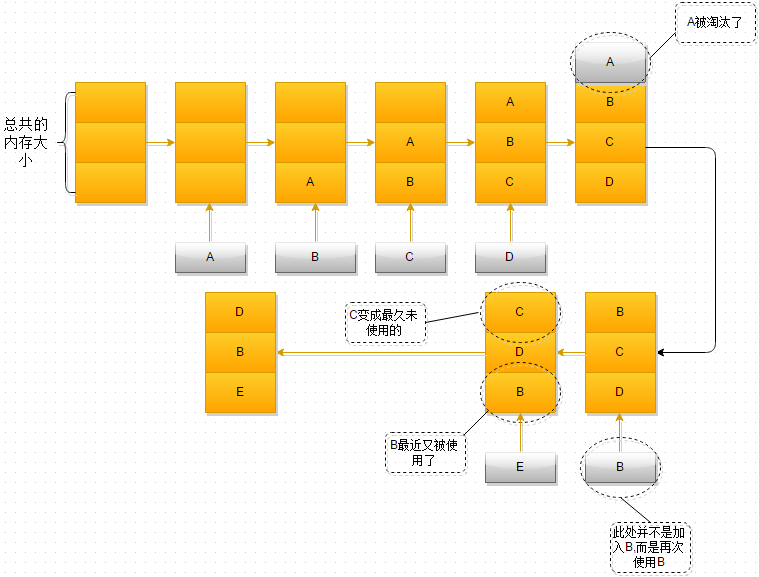
- 最开始时,内存空间是空的,因此依次进入A、B、C是没有问题的
- 当加入D时,就出现了问题,内存空间不够了,因此根据LRU算法,内存空间中A待的时间最为久远,选择A,将其淘汰
- 当再次引用B时,内存空间中的B又处于活跃状态,而C则变成了内存空间中,近段时间最久未使用的
- 当再次向内存空间加入E时,这时内存空间又不足了,选择在内存空间中待的最久的C将其淘汰出内存,这时的内存空间存放的对象就是E->B->D
二、LRU 算法设计
最开始我是这样写的: 没有使用双向链表,导致 adjust 函数的时间复杂度达到了O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class LRUCache {
private int capacity;
int size;
private HashMap<Integer, Integer> map = new HashMap<>();
private ArrayDeque<Integer> KEY = new ArrayDeque<>();
public LRUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
}
public int get(int key) {
if(map.containsKey(key))
{
adjust(key);
return map.get(key);
}
return -1;
}
public void adjust(int key)
{
KEY.remove(key);
KEY.offer(key);
}
public void put(int key, int value) {
if(map.containsKey(key))
{
adjust(key);
}
else
{
size++;
KEY.offer(key);
}
map.put(key, value);
if(size > capacity)
{
map.remove(KEY.poll());
size--;
}
}
}
|
LRU 更好的设计是使用双向链表+HashMap
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
class LRUCache {
private DoubleList cache;
private HashMap<Integer, Node> map;
private int size;
private int capacity;
public LRUCache(int capacity) {
cache = new DoubleList();
map = new HashMap<Integer, Node>();
size = 0;
this.capacity = capacity;
}
public int get(int key) {
if (!map.containsKey(key))
return -1;
Node node = map.get(key);
cache.remove(node);
cache.add(node);
return node.val;
}
public void adjust(Node node) {
cache.remove(node);
cache.add(node);
}
public void put(int key, int value) {
Node node;
if (map.containsKey(key)) {
node = map.get(key);
cache.remove(node);
} else {
if (size == capacity) {
node = cache.getHead();
map.remove(node.key);
cache.remove(node);
size--;
}
size++;
}
node = new Node(key, value);
cache.add(node);
map.put(key, node);
}
}
class Node {
int key, val;
Node prev;
Node next;
Node(int key, int val) {
this.key = key;
this.val = val;
}
Node() {}
}
class DoubleList {
private Node dummyHead = new Node(0, 0), tail = dummyHead;
public void add(Node x) {
tail.next = x;
x.prev = tail;
tail = x;
}
public void remove(Node x) {
x.prev.next = x.next;
if (x.next != null) {
x.next.prev = x.prev;
} else {
tail = x.prev;
}
x.prev = null;
x.next = null;
}
public Node getHead() {
return dummyHead.next;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/
|
三、LFU 缓存机制概念
LRU 算法的淘汰策略是 Least Recently Used,也就是每次淘汰那些最久没被使用的数据;而 LFU 算法的淘汰策略是 Least Frequently Used,也就是每次淘汰那些使用次数最少的数据。
从实现难度上来说,LFU 算法的难度大于 LRU 算法,因为 LRU 算法相当于把数据按照时间排序,这个需求借助链表很自然就能实现,你一直从链表头部加入元素的话,越靠近头部的元素就是新的数据,越靠近尾部的元素就是旧的数据,我们进行缓存淘汰的时候只要简单地将尾部的元素淘汰掉就行了。
而 LFU 算法相当于是把数据按照访问频次进行排序,这个需求恐怕没有那么简单,而且还有一种情况,如果多个数据拥有相同的访问频次,我们就得删除最早插入的那个数据。也就是说 LFU 算法是淘汰访问频次最低的数据,如果访问频次最低的数据有多条,需要淘汰最旧的数据。
四、LFU 算法设计


上图就是实现过程:1, 2, 3等表示频率。与这两张图完全一样的是解法二。
使用双哈希结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
class LFUCache {
HashMap<Integer, Integer> keyToValue;
HashMap<Integer, Integer> keyToFreq;
HashMap<Integer, LinkedHashSet<Integer>> freqToKeys;
int minFreq;
int size;
int capacity;
public LFUCache(int capacity) {
this.capacity = capacity;
size = 0;
minFreq = Integer.MAX_VALUE;
keyToValue = new HashMap<>();
keyToFreq = new HashMap<>();
freqToKeys = new HashMap<>();
}
public int get(int key) {
if (!keyToValue.containsKey(key))
return -1;
increaseFreq(key);
return keyToValue.get(key);
}
public void increaseFreq(int key) {
int preFreq = keyToFreq.getOrDefault(key, 0);
keyToFreq.put(key, preFreq + 1);
if (preFreq != 0) {
LinkedHashSet<Integer> set = freqToKeys.get(preFreq);
set.remove(key);
if (set.isEmpty()) {
freqToKeys.remove(preFreq);
if (minFreq == preFreq)
minFreq = preFreq + 1;
}
} else {
minFreq = 1;
}
if (!freqToKeys.containsKey(preFreq+1)) {
LinkedHashSet<Integer> set = new LinkedHashSet<>();
freqToKeys.put(preFreq+1, set);
}
freqToKeys.get(preFreq+1).add(key);
}
public void put(int key, int value) {
if (!keyToValue.containsKey(key)) {
if (size == capacity) {
if (size == 0)
return;
LinkedHashSet<Integer> set = freqToKeys.get(minFreq);
int deletedKey = set.iterator().next();
set.remove(deletedKey);
keyToValue.remove(deletedKey);
keyToFreq.remove(deletedKey);
if (set.isEmpty()) {
freqToKeys.remove(minFreq);
}
size--;
}
size++;
}
keyToValue.put(key, value);
increaseFreq(key);
}
}
|
O(1) 解法 —— 存储频次的HashMap改为直接用双向链表(最优实现 13ms 双100%)来自
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
|
class LFUCache {
Map<Integer, Node> cache; // 存储缓存的内容,Node中除了value值外,还有key、freq、所在doublyLinkedList、所在doublyLinkedList中的postNode、所在doublyLinkedList中的preNode,具体定义在下方。
DoublyLinkedList firstLinkedList; // firstLinkedList.post 是频次最大的双向链表
DoublyLinkedList lastLinkedList; // lastLinkedList.pre 是频次最小的双向链表,满了之后删除 lastLinkedList.pre.tail.pre 这个Node即为频次最小且访问最早的Node
int size;
int capacity;
public LFUCache(int capacity) {
cache = new HashMap<> (capacity);
firstLinkedList = new DoublyLinkedList();
lastLinkedList = new DoublyLinkedList();
firstLinkedList.post = lastLinkedList;
lastLinkedList.pre = firstLinkedList;
this.capacity = capacity;
}
public int get(int key) {
Node node = cache.get(key);
if (node == null) {
return -1;
}
// 该key访问频次+1
freqInc(node);
return node.value;
}
public void put(int key, int value) {
if (capacity == 0) {
return;
}
Node node = cache.get(key);
// 若key存在,则更新value,访问频次+1
if (node != null) {
node.value = value;
freqInc(node);
} else {
// 若key不存在
if (size == capacity) {
// 如果缓存满了,删除lastLinkedList.pre这个链表(即表示最小频次的链表)中的tail.pre这个Node(即最小频次链表中最先访问的Node),如果该链表中的元素删空了,则删掉该链表。
cache.remove(lastLinkedList.pre.tail.pre.key);
lastLinkedList.removeNode(lastLinkedList.pre.tail.pre);
size--;
if (lastLinkedList.pre.head.post == lastLinkedList.pre.tail) {
removeDoublyLinkedList(lastLinkedList.pre);
}
}
// cache中put新Key-Node对儿,并将新node加入表示freq为1的DoublyLinkedList中,若不存在freq为1的DoublyLinkedList则新建。
Node newNode = new Node(key, value);
cache.put(key, newNode);
if (lastLinkedList.pre.freq != 1) {
DoublyLinkedList newDoublyLinedList = new DoublyLinkedList(1);
addDoublyLinkedList(newDoublyLinedList, lastLinkedList.pre);
newDoublyLinedList.addNode(newNode);
} else {
lastLinkedList.pre.addNode(newNode);
}
size++;
}
}
/**
* node的访问频次 + 1
*/
void freqInc(Node node) {
// 将node从原freq对应的双向链表里移除, 如果链表空了则删除链表。
DoublyLinkedList linkedList = node.doublyLinkedList;
DoublyLinkedList preLinkedList = linkedList.pre;
linkedList.removeNode(node);
if (linkedList.head.post == linkedList.tail) {
removeDoublyLinkedList(linkedList);
}
// 将node加入新freq对应的双向链表,若该链表不存在,则先创建该链表。
node.freq++;
if (preLinkedList.freq != node.freq) {
DoublyLinkedList newDoublyLinedList = new DoublyLinkedList(node.freq);
addDoublyLinkedList(newDoublyLinedList, preLinkedList);
newDoublyLinedList.addNode(node);
} else {
preLinkedList.addNode(node);
}
}
/**
* 增加代表某1频次的双向链表
*/
void addDoublyLinkedList(DoublyLinkedList newDoublyLinedList, DoublyLinkedList preLinkedList) {
newDoublyLinedList.post = preLinkedList.post;
newDoublyLinedList.post.pre = newDoublyLinedList;
newDoublyLinedList.pre = preLinkedList;
preLinkedList.post = newDoublyLinedList;
}
/**
* 删除代表某1频次的双向链表
*/
void removeDoublyLinkedList(DoublyLinkedList doublyLinkedList) {
doublyLinkedList.pre.post = doublyLinkedList.post;
doublyLinkedList.post.pre = doublyLinkedList.pre;
}
}
class Node {
int key;
int value;
int freq = 1;
Node pre; // Node所在频次的双向链表的前继Node
Node post; // Node所在频次的双向链表的后继Node
DoublyLinkedList doublyLinkedList; // Node所在频次的双向链表
public Node() {}
public Node(int key, int value) {
this.key = key;
this.value = value;
}
}
class DoublyLinkedList {
int freq; // 该双向链表表示的频次
DoublyLinkedList pre; // 该双向链表的前继链表(pre.freq < this.freq)
DoublyLinkedList post; // 该双向链表的后继链表 (post.freq > this.freq)
Node head; // 该双向链表的头节点,新节点从头部加入,表示最近访问
Node tail; // 该双向链表的尾节点,删除节点从尾部删除,表示最久访问
public DoublyLinkedList() {
head = new Node();
tail = new Node();
head.post = tail;
tail.pre = head;
}
public DoublyLinkedList(int freq) {
head = new Node();
tail = new Node();
head.post = tail;
tail.pre = head;
this.freq = freq;
}
void removeNode(Node node) {
node.pre.post = node.post;
node.post.pre = node.pre;
}
void addNode(Node node) {
node.post = head.post;
head.post.pre = node;
head.post = node;
node.pre = head;
node.doublyLinkedList = this;
}
}
|



