KMP算法理解

一、朴素匹配方法

参考宫水三页题解

1
2
3


约定

本文用 pat 表示模式串，长度为 M，txt 表示文本串，长度为 N。KMP 算法是在 txt 中查找子串 pat，如果存在，返回这个子串的起始索引，否则返回 -1

直观的解法的是：枚举文本串 txt 中的每个字符作为「发起点」，每次从文本串的「发起点」和匹配串的「首位」开始尝试匹配：

匹配成功：返回本次匹配的文本串「发起点」。匹配失败：枚举文本串的下一个「发起点」，重新尝试匹配。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
    public int strStr(String ss, String pp) {
        int n = ss.length(), m = pp.length();
        char[] s = ss.toCharArray(), p = pp.toCharArray();
        // 枚举原串的「发起点」
        for (int i = 0; i <= n - m; i++) {
            // 从原串的「发起点」和匹配串的「首位」开始，尝试匹配
            int a = i, b = 0;
            while (b < m && s[a] == p[b]) {
                a++;
                b++;
            }
            // 如果能够完全匹配，返回原串的「发起点」下标
            if (b == m) return i;
        }
        return -1;
    }
}

时间复杂度 O((M - N) * N)

二、KMP 算法

KMP 算法是一个快速查找匹配串的算法，它的作用其实就是本题问题：如何快速在「原字符串」中找到「匹配字符串」。

上述的朴素解法，不考虑剪枝的话复杂度是 O(m * n) 的，而 KMP 算法的复杂度为 O(m + n)。

KMP 之所以能够在 O(m + n)O(m+n) 复杂度内完成查找，是因为其能在「非完全匹配」的过程中提取到有效信息进行复用，以减少「重复匹配」的消耗。

1. 最长前缀、后缀匹配长度

在模拟 KMP 匹配过程之前，我们先建立两个概念：

前缀：对于字符串 abcxxxxefg，我们称 abc 属于 abcxxxxefg 的某个前缀。后缀：对于字符串 abcxxxxefg，我们称 efg 属于 abcxxxxefg 的某个后缀。

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

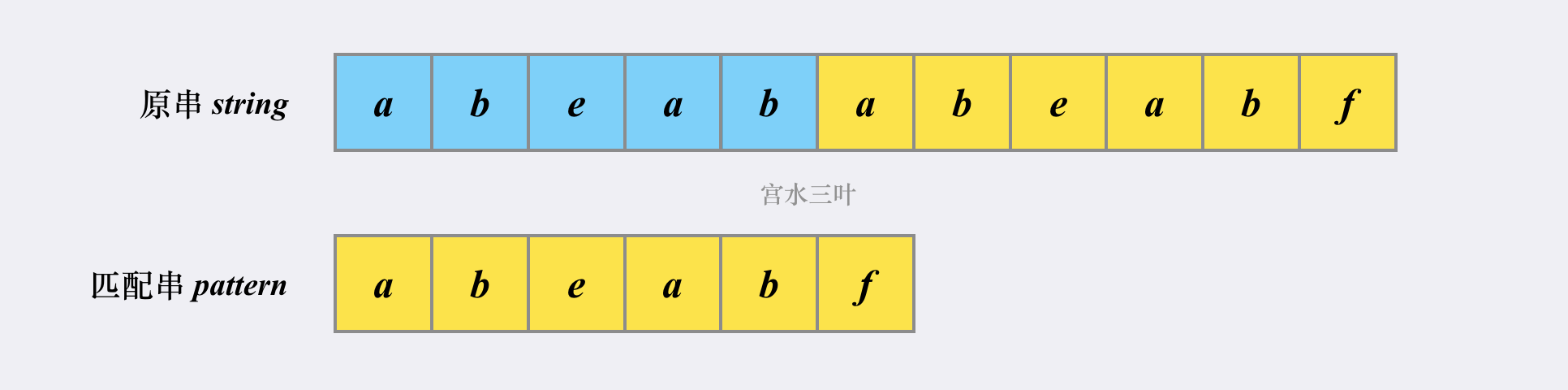
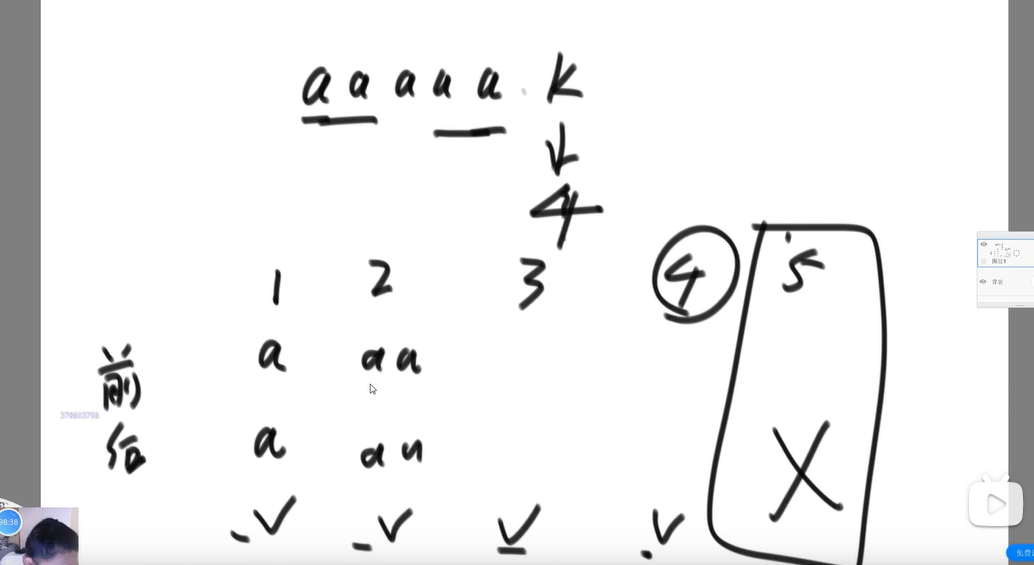
最长匹配长度例子：

匹配串：aaaaak，对于k这个字符来讲最长匹配长度就是4

2. 前缀表与 next 数组

举个例子

1
2


模式串：[aabaabsaabaabst]
next:  [-1 0 1 0 1 2 3 ...]

对于这个模式串

i = 0 时：前面没有串规定为-1

i = 1 时：前面的串为“a", 最长匹配长度为0

i = 2 时：前面的串为”aa", 最长匹配长度为1

3. 理解 KMP 如何利用next数组加速

先来看看朴素匹配过程

将原串的指针移动至本次「发起点」的下一个位置（b 字符处）；匹配串的指针移动至起始位置。
尝试匹配，发现对不上，原串的指针会一直往后移动，直到能够与匹配串对上位置。

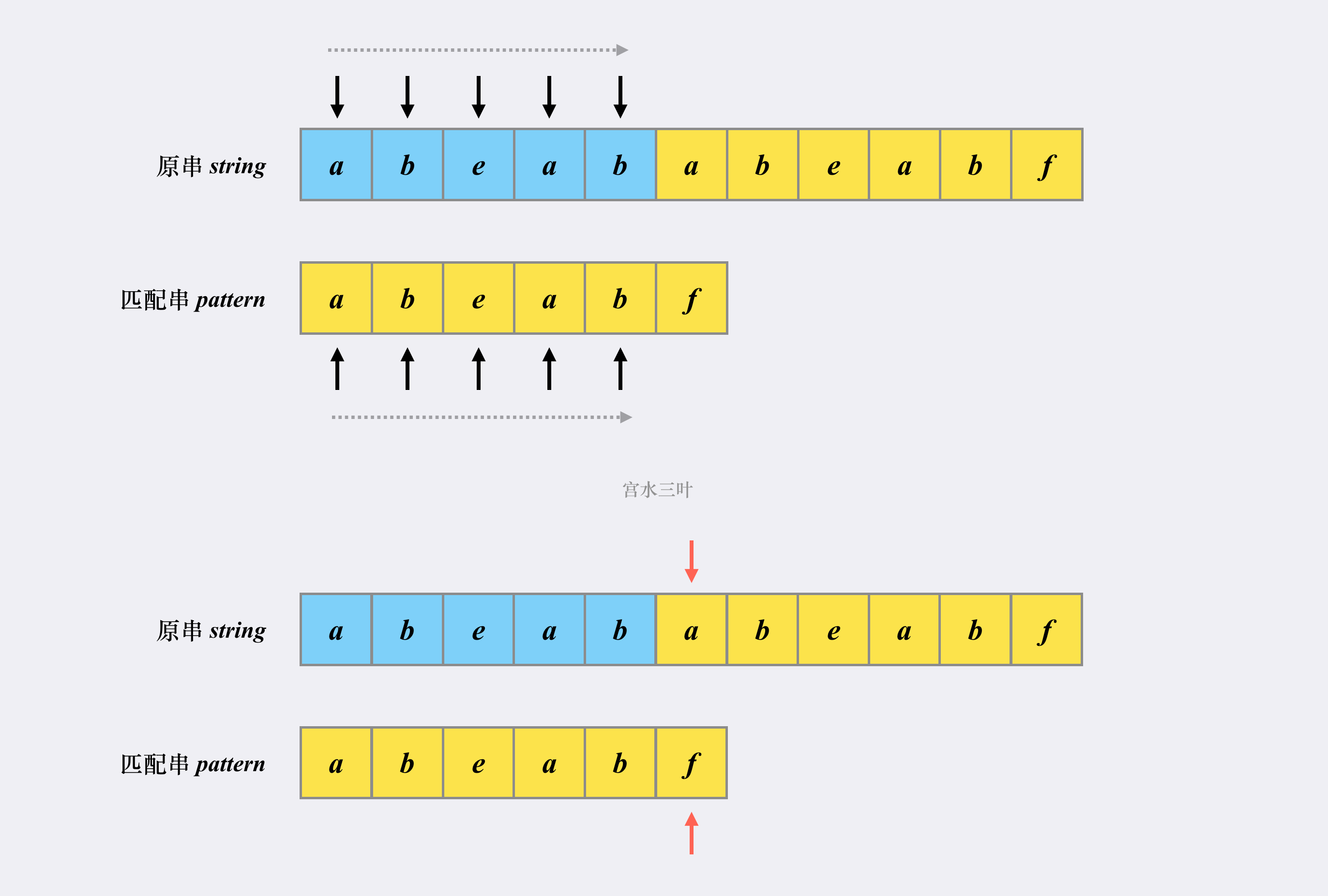
再红标处不匹配，这时朴素做法是认为i = 0 的发起点无法匹配模式串，则i++，跳转到下一个发起点进行匹配。

再来看看KMP 匹配的做法

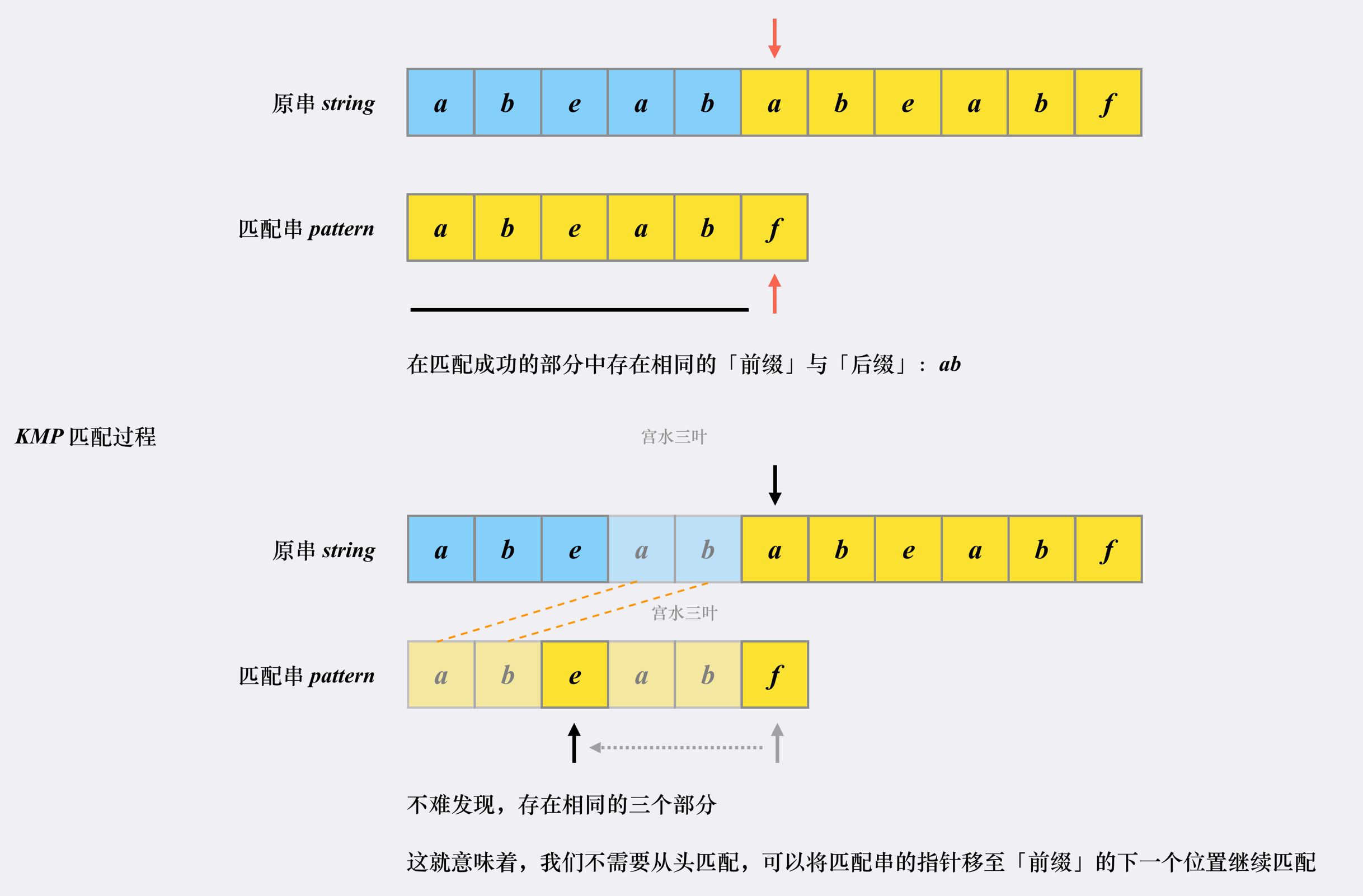
首先匹配串会检查之前已经匹配成功的部分中里是否存在相同的「前缀」和「后缀」。如果存在，则跳转到「前缀」的下一个位置继续往下匹配：

原因是匹配串发起点不会出现在后缀的起点之前。（反证法）

以下面的例子说明：

开始知道了i = 0 为发起点，无法匹配。f 点最长前缀为2

i = 1，必然配不出来

i = 2，必然配不出来。

i = 3，才有可能。

4. 代码实现（不包括next 数组的求法）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


public static int getIndexOf(String s, String m) {
    if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
    	return -1;
    }
    char[] str1 = s.toCharArray();
    char[] str2 = m.toCharArray();
    int i1 = 0;
    int i2 = 0;
    int[] next = getNextArray(str2);
    while (i1 < str1.length && i2 < str2.length) {
        if (str1[i1] == str2[i2]) {
            i1++;
            i2++;
        } else if (next[i2] == -1) { // i2 == 0
            i1++;
        } else {
            i2 = next[i2];
        }
    }
    return i2 == str2.length ? i1 - i2 : -1;
}

5. next 数组求解

动态规划

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


public static int[] getNextArray(char[] ms) {
    if (ms.length == 1) {
        return new int[] {-1};
    }
    int[] next = new int[ms.length];
    next[0] = -1;
    next[1] = 0;
    int i = 2;
    int cn = 0;		//  ms的第cn个字符
    while (i < next.length) {
        if (ms[i-1] == ms[cn]) {
            next[i++] = ++cn;
        } else if (cn > 0) {
            cn = next[cn];
        } else {
            next[i++] = 0;
        }
    }
    return next;
}