一、图的逻辑结构和具体实现
面试笔试很少出现图相关的问题,就算有,大多也是简单的遍历问题。图这部分的内容关注最实用的,不去纠结图相关的复杂算法。
图数据结构很简单,相关定义也很熟悉了,这里就不重复了,直接看图数据结构的存储。
形成一套java 的可复用图结构数据定义。
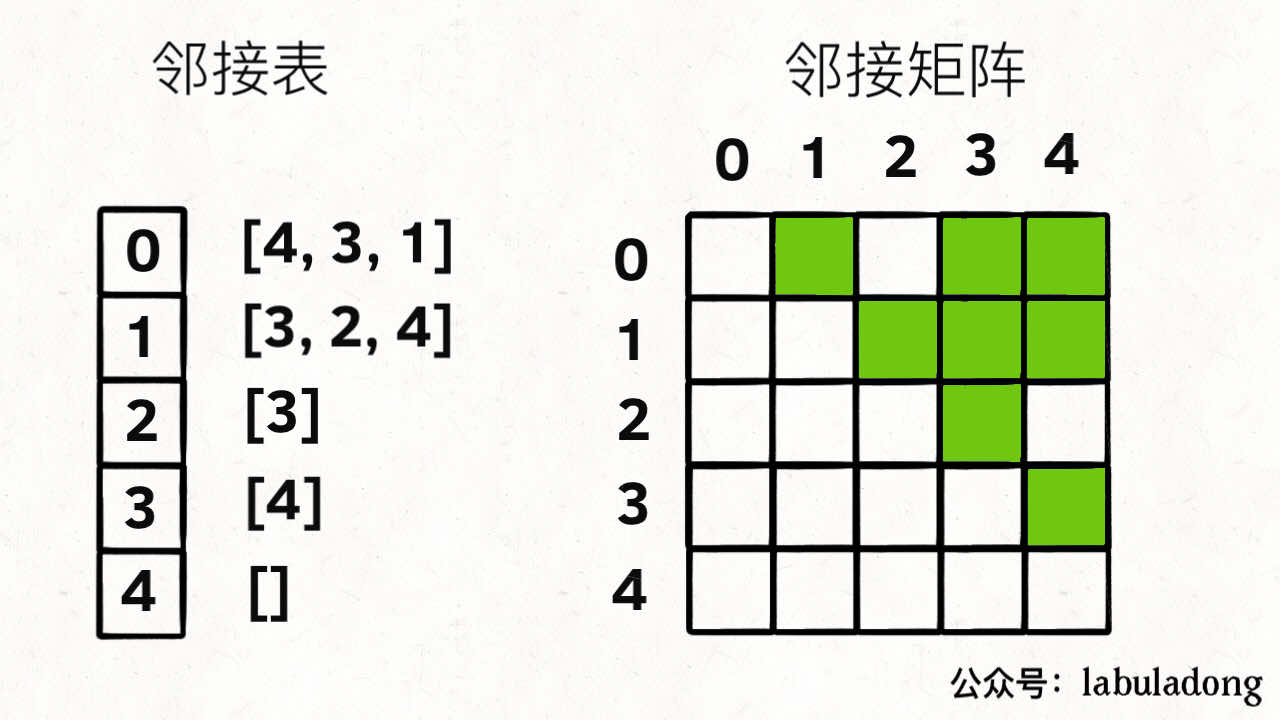
一般的图存储方式就是邻接表和邻接矩阵。

对于这张图,用邻接表和邻接矩阵的存储方式如下:
Node.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
public class Node {
public int value;
public int in;
public int out;
public ArrayList<Node> nexts;
public ArrayList<Edge> edges;
public Node (int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
|
Edge.java
1
2
3
4
5
6
7
8
9
10
11
|
public class Edge {
public int weight;
public Node from;
public Node to;
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
|
Graph.java
1
2
3
4
5
6
7
8
9
|
public class Graph {
public HashMap<Integer, Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
|
GraphGenerator
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public static Graph createGraph(int[][] matrix) {
Graph graph = new Graph();
for (int i = 0; i < matrix.length; i++) {
int from = matrix[i][0];
int to = matrix[i][1];
int weight = matrix[i][2];
if (!graph.nodes.containsKey(from))
graph.nodes.put(from, new Node(from));
if (!graph.nodes.containsKey(to))
graph.nodes.put(to, new Node(to));
Node fromNode = graph.nodes.get(from), toNode = graph.nodes.get(to);
Edge newEdge = new (weight, fromNode, toNode);
graph.edges.add(newEdge);
fromNode.out++;
fromNode.nexts.add(toNode);
fromNode.edges.add(newEdge);
toNode.in++;
}
}
|
根据问题进行结构创建
回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
int n = graph.length;
LinkedList<Integer> list = new LinkedList<>();
list.addLast(0);
backtrack(graph, list, 0, n-1);
return res;
}
public void backtrack(int[][] graph, LinkedList<Integer> list, int src, int dst) {
if (src == dst) {
res.add(new LinkedList<Integer>(list));
}
for (int i = 0; i < graph[src].length; i++) {
list.addLast(graph[src][i]);
backtrack(graph, list, graph[src][i], dst);
list.removeLast();
}
}
}
|
还有一种应付常见题的编码方式,利用邻接表,比如下面这种结构:
graph[s] 是一个列表,存储着节点 s 所指向的节点
二、拓扑排序
深度优先遍历
超出了时间限制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
boolean[] onPath;
boolean[] visited;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int from = 0; from < numCourses; from++) {
if (visited[from])
continue;
if(!dfs(graph, from))
return false;
}
return true;
}
boolean dfs(List<Integer>[] graph, int from) {
if (onPath[from])
return false;
if (visited[from])
return true;
onPath[from] = true;
visited[from] = true;
for (int i = 0; i < graph[from].size(); i++) {
if (!dfs(graph, graph[from].get(i)))
return false;
}
onPath[from] = false;
return true;
}
public List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++)
graph[i] = new LinkedList<>();
for (int i = 0; i < prerequisites.length; i++) {
int from = prerequisites[i][1], to = prerequisites[i][0];
graph[from].add(to);
}
return graph;
}
}
|
拓扑排序

拓扑排序直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的,比如上图所有箭头都是朝右的。
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
但是我们这道题和拓扑排序有什么关系呢?
其实也不难看出来,如果把课程抽象成节点,课程之间的依赖关系抽象成有向边,那么这幅图的拓扑排序结果就是上课顺序。将后序遍历的结果进行反转,就是拓扑排序的结果
那么为什么后序遍历的反转结果就是拓扑排序呢?
1
2
3
4
5
6
7
|
void traverse(TreeNode root) {
// 前序遍历代码位置
traverse(root.left)
// 中序遍历代码位置
traverse(root.right)
// 后序遍历代码位置
}
|
二叉树的后序遍历是什么时候?遍历完左右子树之后才会执行后序遍历位置的代码。换句话说,当左右子树的节点都被装到结果列表里面了,根节点才会被装进去。
后序遍历的这一特点很重要,之所以拓扑排序的基础是后序遍历,是因为一个任务必须在等到所有的依赖任务都完成之后才能开始开始执行。
你把每个任务理解成二叉树里面的节点,这个任务所依赖的任务理解成子节点,那你是不是应该先把所有子节点处理完再处理父节点?这是不是就是后序遍历?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
// 记录后序遍历结果
List<Integer> postorder = new ArrayList<>();
// 记录是否存在环
boolean hasCycle = false;
boolean[] visited, onPath;
// 主函数
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
// 遍历图
for (int i = 0; i < numCourses; i++) {
traverse(graph, i);
}
// 有环图无法进行拓扑排序
if (hasCycle) {
return new int[]{};
}
// 逆后序遍历结果即为拓扑排序结果
Collections.reverse(postorder);
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
res[i] = postorder.get(i);
}
return res;
}
// 图遍历函数
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
// 发现环
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
// 前序遍历位置
onPath[s] = true;
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
// 后序遍历位置
postorder.add(s);
onPath[s] = false;
}
// 建图函数
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
// 图中共有 numCourses 个节点
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1];
int to = edge[0];
// 修完课程 from 才能修课程 to
// 在图中添加一条从 from 指向 to 的有向边
graph[from].add(to);
}
return graph;
}
|
利用入度和出度:使用我们的图类数据结构很好实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public static List<Node> sortedTopology(Graph graph) {
HashMap<Node, Integer> inMap = new HashMap<>();
Queue<Node> zeroInQueue = new LinkedList<>();
for (Node node : graph.nodes.values()) {
inMap.put(node, node.in);
if (node.in == 0) {
zeroInQueue.add(node);
}
}
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
Node cur = zeroInQueue.poll();
result.add(cur);
for (Node next : cur.nexts) {
inMap.put(next, inMap.get(next) - 1);
if (inMap.get(next) == 0)
zeroInQueue.add(next);
}
}
return result;
}
|
下面是课程Ⅱ的解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] nexts = new ArrayList[numCourses];
int[] in = new int[numCourses];
for (int i = 0; i < prerequisites.length; i++) {
int from = prerequisites[i][1], to = prerequisites[i][0];
if (nexts[from] == null) {
nexts[from] = new ArrayList<Integer>();
}
nexts[from].add(to);
in[to] += 1;
}
Queue<Integer> zeroIn = new LinkedList<>();
int[] res = new int[numCourses];
int index = 0;
for (int i = 0; i < numCourses; i++) {
if (in[i] == 0)
zeroIn.add(i);
}
while (!zeroIn.isEmpty()) {
int cur = zeroIn.poll();
res[index++] = cur;
if (nexts[cur] != null) {
for (int next : nexts[cur]) {
in[next]--;
if (in[next] == 0)
zeroIn.add(next);
}
}
}
if (index != numCourses)
return new int[]{};
return res;
}
}
|
三、二分图的判定
3.1 二分图概念
二分图的顶点集可分割为两个互不相交的子集,图中每条边依附的两个顶点都分属于这两个子集,且两个子集内的顶点不相邻。
给你一幅「图」,请你用两种颜色将图中的所有顶点着色,且使得任意一条边的两个端点的颜色都不相同,你能做到吗?
这就是图的「双色问题」,其实这个问题就等同于二分图的判定问题,如果你能够成功地将图染色,那么这幅图就是一幅二分图,反之则不是:

3.2 判断方法
直接就是遍历,为每个节点设置颜色标志,并进行判断。直到所有的节点都被访问停止。具体有DFS 和 BFS, 都可以实现,没什么难度。
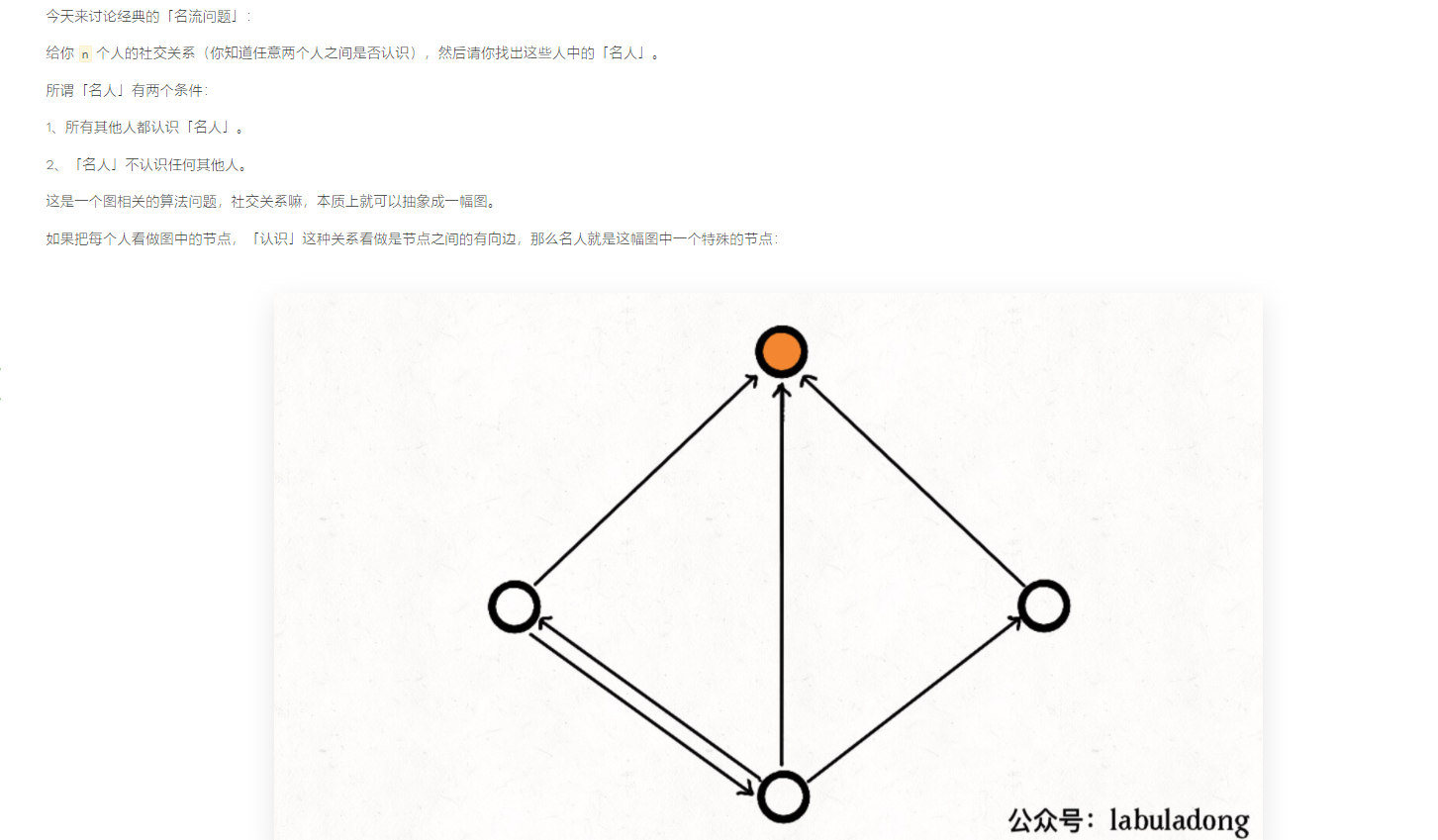
四、名流问题
-
这种题直接使用图的入度和出度遍历即可。
-
也可以使用候选人的方式进行筛选。对于每一组候选者,都可以排除一个候选人。




