动态规划背包问题

一、0-1背包

有一个容量为 N 的背包，要用这个背包装下物品的价值最大，这些物品有两个属性：体积 w 和价值 v。

定义一个二维数组 dp 存储最大价值，其中 dp [i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i 件物品体积为 w，价值为 v，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：

第 i 件物品没添加到背包，总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值，dp[i][j] = dp[i-1][j]。
第 i 件物品添加到背包中，dp[i][j] = dp[i-1][j-w] + v。

第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。因此，0-1 背包的状态转移方程为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// W 为背包总体积
// N 为物品数量
// weights 数组存储 N 个物品的重量
// values 数组存储 N 个物品的价值
public int knapsack(int W, int N, int[] weights, int[] values) {
    int[][] dp = new int[N + 1][W + 1];
    for (int i = 1; i <= N; i++) {
        int w = weights[i - 1], v = values[i - 1];
        for (int j = 1; j <= W; j++) {
            if (j >= w) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[N][W];
}

无法使用贪心算法的解释

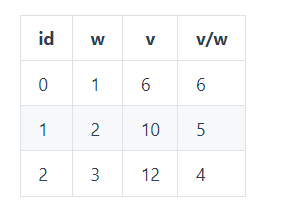
0-1 背包问题无法使用贪心算法来求解，也就是说不能按照先添加性价比最高的物品来达到最优，这是因为这种方式可能造成背包空间的浪费，从而无法达到最优。考虑下面的物品和一个容量为 5 的背包，如果先添加物品 0 再添加物品 1，那么只能存放的价值为 16，浪费了大小为 2 的空间。最优的方式是存放物品 1 和物品 2，价值为 22.

优化空间复杂度

空间 V 按照递减顺序进行。

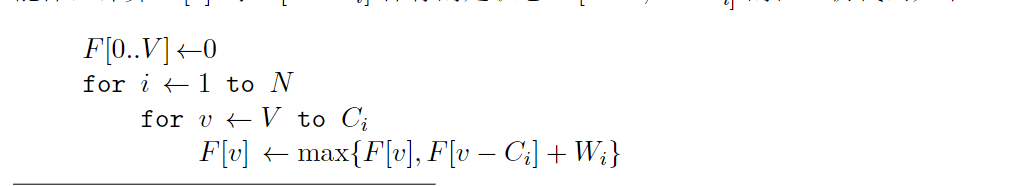
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// W 为背包总体积
// N 为物品数量
// weights 数组存储 N 个物品的重量
// values 数组存储 N 个物品的价值
public int knapsack(int W, int N, int[] weights, int[] values) {
    int[] dp = new int[W + 1];
    for (int i = 1; i <= N; i++) {
        int w = weights[i - 1], v = values[i - 1];
        for (int j = W; j >= 0; j--) {
            if (j >= w) {
                dp[j] = Math.max(dp[j], dp[j-w] + v);
            } else {
                dp[j] = dp[j];
            }
        }
    }
    return dp[W];
}

初始化

恰好装满背包的要求，初始化如下：$F[0] = 0, F[1…V] = - \infty $

二、完全背包

有 N 种物品和一个容量为 V 的背包，每种物品都有无限件可用。放入第 i 种物品的费用是 Ci，价值是 Wi。求解：将哪些物品装入背包，可使这些物品的耗费的费用总和不超过背包容量，且价值总和最大。

1. 基本思路

F [i, v] 表示前 i 种物品恰放入一个容量为 v 的背包的最大权值

状态转移
$$ F [i, v] = max{F [i −1, v −kCi] + kWi |0 ≤kCi ≤v} $$

可以使用转化为01 背包问题求解，利用二进制思想，因为，不管最优策略选几件第 i 种物品，其件数写成二进制后，总可以表示成若干个 2k 件物品的和。这样一来就把每种物品拆成 O(log ⌊V /Ci⌋) 件物品，是一个很大的改进。

2. O(VN) 的算法

状态转移不同 $$ F[i,v] = max(F[i-1, v], F[i, v-Ci] + Wi) $$ 每次转移表示是否接受第 i 种物品的一个新实例。F[i, v] 可能代表 v 容量背包内存在第 i 种物品，也可能不存在。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


// AcWing
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt(), V = reader.nextInt();
        int[] volume = new int[N];
        int[] weight = new int[N];
        for (int i = 0; i < N; i++) {
            volume[i] = reader.nextInt();
            weight[i] = reader.nextInt();
        }
        reader.close();
        
        int[] dp = new int[V+1];
        for (int i = 0; i < N; i++) {
            for (int j = volume[i]; j <= V; j++) {
                dp[j] = Math.max(dp[j], dp[j-volume[i]] + weight[i]);
            }
        }
        System.out.println(dp[V]);
    }
}

三、多重背包

有 N 种物品和一个容量为 V 的背包。第 i 种物品最多有 Mi 件可用，每件耗费的空间是 Ci，价值是 Wi。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可。因为对于第 i 种物品有 Mi + 1 种策略：取 0 件，取 1 件……取 Mi 件。令 F [i, v] 表示前 i 种物品恰放入一个容量为 v 的背包的最大价值，则有状态转移方程： $$ F [i，v] = max{F [i −1, v −k ∗Ci] + k ∗Wi |0 ≤k ≤Mi} $$

复杂度是 O(V ΣMi)。

1. 二进制优化方法

利用二进制的思想

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


// AcWing
import java.util.Scanner;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt(), V = reader.nextInt();
        int[] volume = new int[N];
        int[] weight = new int[N];
        int[] limit = new int[N];
        for (int i = 0; i < N; i++) {
            volume[i] = reader.nextInt();
            weight[i] = reader.nextInt();
            limit[i] = reader.nextInt();
        }
        reader.close();
        
        ArrayList<Integer> newVolume = new ArrayList<>();
        ArrayList<Integer> newWeight = new ArrayList<>();
        for (int i = 0; i < N; i++) {
            int m = limit[i];
            int k = 1;
            while (m - k > 0) {
                m -= k;
                newVolume.add(k * volume[i]);
                newWeight.add(k * weight[i]);
                k *= 2;
            }
            newVolume.add(m * volume[i]);
            newWeight.add(m * weight[i]);
        }
        int n = newWeight.size();
        int[] dp = new int[V+1];
        for (int i = 0; i < n; i++) {
            for (int j = V; j >= newVolume.get(i); j--) {
                dp[j] = Math.max(dp[j], dp[j-newVolume.get(i)] + newWeight.get(i));
            }
        }
        System.out.println(dp[V]);
    }
}

2. 单调队列优化方法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


// AcWing
import java.util.Scanner;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt(), V = reader.nextInt();
        int[] dp = new int[V+1];
        int[] queue = new int[V+1];
        int[] nums = new int[V+1];
        for (int i = 0; i < N; i++) {
            int v = reader.nextInt();
            int w = reader.nextInt();
            int s = reader.nextInt();
            for (int j = 0; j < v; j++) {
                int head = 0, tail = -1;
                for (int k = 0; j + v * k <= V; k++) {
                    int tmp = dp[j + k * v] - k * w;
                    while (head <= tail && k - nums[head] > s) head++;
                    while (head <= tail && queue[tail] <= tmp) tail--;
                    queue[++tail] = tmp;
                    nums[tail] = k;
                    dp[j + v * k] = queue[head] + k * w;
                }
            }
        }
        System.out.println(dp[V]);
    }
}

四、混合背包

如果将前面1、2、3中的三种背包问题混合起来。也就是说，有的物品只可以取一次（01 背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背包）。应该怎么求解呢？

结合上述3类问题的解法即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


// AcWing
import java.util.Scanner;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt(), V = reader.nextInt();
        int[] dp = new int[V+1];
        for (int i = 0; i < N; i++) {
            int v = reader.nextInt();
            int w = reader.nextInt();
            int s = reader.nextInt();
            if (s == -1) {
                for (int j = V; j >= v; j--) {
                    dp[j] = Math.max(dp[j], dp[j - v] + w);
                }
            } else if (s == 0) {
                for (int j = v; j <= V; j++) {
                    dp[j] = Math.max(dp[j], dp[j - v] + w);
                }
            } else {
                int[] queue = new int[V+1];
                int[] nums = new int[V+1];
                for (int j = 0; j < v; j++) {
                    int head = 0, tail = -1;
                    for (int k = 0; j + k * v <= V; k++) {
                        int tmp = dp[j + k * v] - k * w;
                        while (head <= tail && k - nums[head] > s) head++;
                        while (head <= tail && queue[tail] <= tmp) tail--;
                        queue[++tail] = tmp;
                        nums[tail] = k;
                        dp[j + k * v] = queue[head] + k * w;
                    }
                }
            }
        }
        System.out.println(dp[V]);
    }
}

五、二维费用的背包

二维费用的背包问题是指：对于每件物品，具有两种不同的费用，选择这件物品必须同时付出这两种费用。对于每种费用都有一个可付出的最大值（背包容量）。问怎样选择物品可以得到最大的价值。设第 i 件物品所需的两种费用分别为 Ci 和 Di。两种费用可付出的最大值（也即两种背包容量）分别为 V 和 U 。物品的价值为 Wi。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt();
        int V = reader.nextInt();
        int M = reader.nextInt();
        int[][] dp = new int[V+1][M+1];
        for (int i = 0; i < N; i++) {
            int v = reader.nextInt();
            int m = reader.nextInt();
            int w = reader.nextInt();
            for (int j = V; j >= v; j--) {
                for (int k = M; k >= m; k--) {
                    dp[j][k] = Math.max(dp[j][k], dp[j-v][k-m] + w);
                }
            }
        }
        System.out.println(dp[V][M]);
    }
}

六、分组的背包问题

有 N 件物品和一个容量为 V 的背包。第 i 件物品的费用是 Ci，价值是 Wi。这些物品被划分为 K 组，每组中的物品互相冲突，最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        int N = reader.nextInt();
        int V = reader.nextInt();
        int[] dp = new int[V+1];
        for (int i = 0; i < N; i++) {
            int S = reader.nextInt();
            int[] arrV = new int[S];
            int[] arrW = new int[S];
            for (int k = 0; k < S; k++) {
                arrV[k] = reader.nextInt();
                arrW[k] = reader.nextInt();
            }
            for (int j = V; j >= 0; j--) {
                for (int k = 0; k < S; k++) {
                    int v = arrV[k], w = arrW[k];
                    if (j - v >= 0) {
                        dp[j] = Math.max(dp[j], dp[j-v] + w);
                    }
                }
            }
        }
        System.out.println(dp[V]);
    }
}

七、有依赖的背包

1. 简化的问题

这种背包问题的物品间存在某种“依赖”的关系。也就是说，物品 i 依赖于物品 j，表示若选物品 i，则必须选物品 j。为了简化起见，我们先设没有某个物品既依赖于别的物品，又被别的物品所依赖；另外，没有某件物品同时依赖多件物品。

对附件组进行01 背包处理，变为分组问题。

2. 较一般的问题

更一般的问题是：依赖关系以图论中“森林”3的形式给出。也就是说，主件的附件仍然可以具有自己的附件集合。限制只是每个物品最多只依赖于一个物品（只有一个主件）且不出现循环依赖。

采用树形DP、将每一个子树root节点利用附件集合 0 1 背包进行处理

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


import java.util.*;

public class Main {
    private static HashMap<Integer, List<Integer>> map = new HashMap<>();
    private static int N;
    private static int V;
    private static int[] volume;
    private static int[] weight;
    private static int[][] dp;

    public static void main(String[] args) {
        Scanner reader = new Scanner(System.in);
        N = reader.nextInt();
        V = reader.nextInt();
        volume = new int[N];
        weight = new int[N];
        dp = new int[N][V+1];
        int root = 0;
        for (int i = 0; i < N; i++) {
            volume[i] = reader.nextInt();
            weight[i] = reader.nextInt();
            int p = reader.nextInt();
            if (p != -1) {
                List<Integer> list = map.getOrDefault(p-1, new LinkedList<Integer>());
                list.add(i);
                map.put(p-1, list);
            } else {
                root = i;
            }
        }
        dfs(root);
        System.out.println(dp[root][V]);

    }

    public static void dfs(int x) {
        for (int i = volume[x]; i <= V; i++)
            dp[x][i] = weight[x];
        List<Integer> list = map.get(x);
        for (int i = 0; list != null && i < list.size(); i++) {
            int y = list.get(i);
            dfs(y);
            for (int j = V; j >= volume[x]; j--) {
                for (int k = 0; k <= j - volume[x]; k++)
                    dp[x][j] = Math.max(dp[x][j], dp[y][k] + dp[x][j - k]);
            }
        }
    }
}